先週（1/18）の解答 H23 年度 星陵高校（英数総合コース）

この問題は　H23 年度　星陵高校（英数総合コース）　の入試問題 　です。

よく出題される基本問題なので、一回解いておけば、パターンは同じですから他の問題でも解けるようになります。

☆解答☆

ポイント　　必ず展開図を書いて扇形の中心角を求める




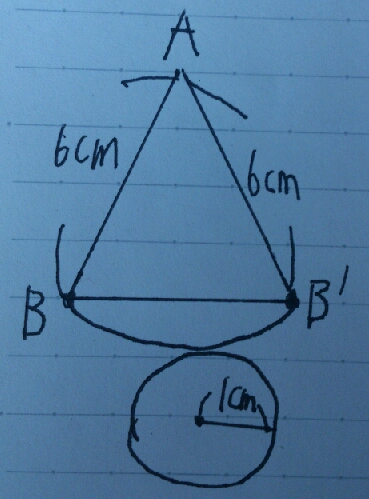
線の長さが最も短くなるのは上の展開図で、B―B'　の場合ですので、B―B'　の長さを求めればよいことになります。

ここで扇型ABB'（三角形ABB'）の中心角Aの角度ですが、

360°×ABを半径とする円周分の底面の円周

となります。

従って、　360°×6cm×2×π分の1ｃｍ×2×π＝360°×6分の1＝60°　　です。

ABとAB'は母線なのでAB=AB'で、しかも中心角が60°なので、三角形ABB'は　正三角形　です。

したがってB―B'　の長さは　6cm　です。


☆　簡単な方法（公式）

　扇形の中心角は　360°×母線分の半径（底面）　で覚えた方が早いです。

また扇形の側面積も　母線×底面の半径×π　（母半π）　を覚えておいた方が得だと思います。



2月上旬に私立高校の入試です。

この時期は過去問を少なくとも10年分以上は解いて、パターン、切り込み口をつかむようにしてください。努力しましょう。